Thickened Flame Model
N. Kim
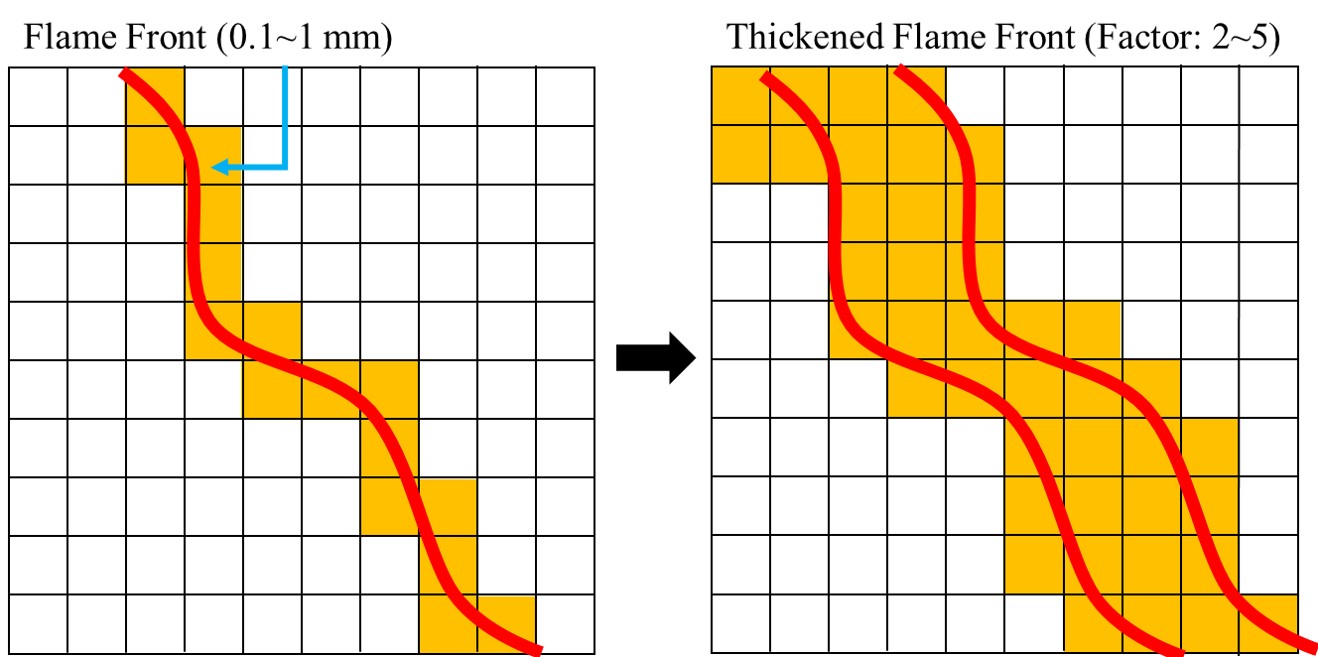
WHAT IS THICKENED FLAME MODEL?
In a practical CFD simulation, a thickness of turublent premixed flame is much smaller than the resolution of computational grid. This means the flame cannot be resolved in the simulation. Obviously, using more refined mesh could be a solution and Adaptive Mesh Refinement could be use to resolve the flame. Another approach to solve this problem is the thickened flame model which automatically detecting flame region and artificially increase thickness of the flame. After the flame is thickened, the thickened flame can be resolved in the computational grid and account for a large scale interaction between flow and flame.
HOW TO IMPLEMENT THIS IDEA?
The flame thickness can be increase by increasing diffusivity($D$) of the species. \begin{equation} \delta \propto \sqrt{D/S_{L}} \label{1} \end{equation} However, merely thickening flame changes flame dynamics, since the flame speed depends on the flame thickness($\delta$) and reaction rate ($\dot{\omega}$). \begin{equation} S_{L} \propto \sqrt{D\dot{\omega}} \label{2} \end{equation} To preserve the flame speed, we increase the diffusivity and decrease reaction rate by multipling F and dividing F, respectively.
\begin{equation} \delta_{F} = F \delta \label{3} \end{equation}
\begin{equation} \dot{\omega_{F}} = 1/F \, \dot{\omega} \label{4} \end{equation}
\begin{equation} S_{L,F} = S_{L} \label{5} \end{equation}
In the thickening process, we actually lose information of small scale flame dynamics. It is analogous to lose pixel information in pooling process in the convolution neural network.
To supplement subgrid scale turbulent-flame interaction, the authors of the model introduce efficiency function $E$.
The efficiency function is the ratio between wrinkling factor with real flame thickness and thickened flame thickness.
\begin{equation}
E = \Xi_{\delta_{l}=\delta} / \Xi_{\delta_{l}=\delta_{F}} \label{6}
\end{equation}
Here, $\Xi$ is the wrinkling factor and it is function of turublent velocity ($u’$), turublent reynolds number $Re_{t}$, test filter length scale $\Delta_{e}$, the flame thickness $\delta_{l}$, and flame speed $S_{L}$.
There are two models for wrinkling factor.
- Colin et. al.: Based on the DNS of flame-vortex interactions.
- Charlette et al.: Based on the power-law expression with equilibrium assumption of flame-surface production and destruction
In the thickened flame model approach, a CFD code solves equations of momentum, species, and energy. The species equation in the thickened flame model can be expressed as follow. \begin{equation} \frac{\partial \rho Y_{i}}{\partial t} + \bigtriangledown \rho \mathbf{u}Y_{i}=\bigtriangledown \cdot (EFD_{i}\bigtriangledown Y_{i})+\frac{E}{F} \dot{\omega_{i}} \label{7} \end{equation}
The Local thickness factor model could be utilized to minimize error caused by modifing diffusivity of the species. \begin{equation} F_{loc} = 1 + (F-1) \Omega(c) \label{8} \end{equation} \begin{equation} \Omega_{c} = 16\left [ c(1-c) \right ]^2 \label{9} \end{equation} \begin{equation} c = Y_{c} / Y_{c,max} \label{10} \end{equation}
Here, $Y_{c}$ is the progress variable, fuel, or oxidizer.
PROS AND CONS
PROS
- Implementation of the model is straight forward: If you have CFD solver for turbulent reactive flow, you have already done 90% of the implementation. You just need to implement the efficiency function and thickness factor.
- The model gives reasonable predictions for both academic and industrial problems.
CONS
- The model modifies heat and mass transfer close to the flame. The fields look like more diffusion dominant than real fields.
- The wrinkling factor model is not universal.
REFERENCES
Fundamentals on Thickened flame model
- O. Colin, f. Ducros, D. Veynante, T.Poinsot, A thickened flame model for large eddy simulations of turbulent premixed combustion, Physics of Fluids 12, 1843 (2000), https://doi.org/10.1063/1.870436
- F. Charlette, C. Meneveau, D. Veynante, A power-law flame wrinkling model for LES of premixed turbulent combustion Part I: non-dynamic formulation and initial tests, Combustion and Flame 131 (2002), https://doi.org/10.1016/S0010-2180(02)00400-5
- F. Charlette, C. Meneveau, D. Veynante,A power-law flame wrinkling model for LES of premixed turbulent combustion Part II: dynamic formulation, Combustion and Flame 131 (2002), https://doi.org/10.1016/S0010-2180(02)00401-7
Applications
- L. Selle, G. Lartigue, T. Poinsot, R. Koch, K.-U.Schildmacher, W. Krebs, B. Prade, P. Kaufmann, D. Veynante, Compressible large eddy simulation of turbulent combustion in complex geometry on unstructured meshes, Combustion and Flame 137 (2004), https://doi.org/10.1016/j.combustflame.2004.03.008
- P. Wolf, G. Staffelbach, L.Y.M. Gicquel, J. Müller, T. Poinsot, Acoustic and Large Eddy Simulation studies of azimuthal modes in annularcombustion chamber, Combustion and Flame 159 (2012), https://doi.org/10.1016/j.combustflame.2012.06.016
Extension for non-premixed turbulent flame
- B. Cueonot, F. Shum-Kivan, S. Blanchard, The thickened flame approach for non-premixed combustion: Principles and implications for turbulent combustion modeling, Combustion and Flame, https://doi.org/10.1016/j.combustflame.2021.111702